Get this post in pdf format here.

Suppose that you have a $k$-form $\alpha$ on a manifold $M$ of dimension $n$. But you’re a spoiled brat and don’t like $k$-forms but rather $(n-k)$-forms, so you go to your dad and throw a tantrum, and your dad says shhh, $k$-forms are okay, see? $k$-forms and $(n-k)$-forms are basically the same, you see, $\Omega^{k}(M)$ and $\Omega^{n-k}(M)$ even have the same dimension, it’s basically the same thing sweetie stop crying everyone’s staring at us please, but you won’t have it because all your friends have $(n-k)$-forms and keep crying, and your dad already spent a lot of money in your $k$-form and $(n-k)$-forms are so expensive! What can your dad do now? He takes your dumb $k$-form to his workshop and comes out three hours later with a shiny $(n-k)$-form, and hands it to you smiling but he’s regretting having children, nay, having you at this point. Oh wow dad, that’s perfect thank you so much you’re the best dad, how did yo do it? Well I told you, $k$-forms and $(n-k)$-forms are not that different, you just need a metric and some patience and you can turn one into the other.

Metric on the exterior algebra

Let $V$ be a finite-dimensional vector space of dimension $n$, and $g$ a Lorentzian metric on $V$, i.e. a symmetric, non-degenerate bilinear map $g:V\times V\to {\mathbb{R}}$. We can extend $g$ bilinearly to $\Lambda^kV$ for any $k$ as

\[g(u_1\wedge\dots\wedge u_k,w_1\wedge\dots\wedge w_k) = \det([g(u_i,w_j)]),\]

where $u_1,\dots,u_k,w_1,\dots,w_k\in V$ and $[g(u_i,w_j)]$ is a matrix whose $(i,j)$-th entry is $g(u_i,w_j)$. For example,

\[g(u_1\wedge u_2,w_1\wedge w_2)=g(u_1,w_1)g(u_2,w_2)-g(u_1,w_2)g(u_2,w_1).\]

Now let $\alpha,\beta \in \Lambda^k V$. With respect to some basis $u^1,\dots,u^n$ of $V$ (not necessarily orthonormal), we can write

\[\begin{aligned} \alpha &= \frac{1}{k!}\alpha_{\mu_1\dots\mu_k}u^{\mu_1}\wedge\dots\wedge u^{\mu_k}\\ \beta &= \frac{1}{k!}\beta_{\mu_1\dots\mu_k}u^{\mu_1}\wedge\dots\wedge u^{\mu_k},\end{aligned}\]

and thus we can find (in Einstein’s notation), writing $g^{ij}=g(u^i,u^j)$ for the components of the metric in this basis,

\[\begin{aligned} g(\alpha,\beta)&= \frac{1}{(k!)^2} \alpha_{\mu_1\dots\mu_k}\beta_{\nu_1\dots\nu_k}\mathrm{det} ( [g(u^{\mu_i},u^{\nu_j})])\\ &= \frac{1}{(k!)^2} \alpha_{\mu_1\dots\mu_k}\beta_{\nu_1\dots\nu_k}\sum_{\sigma\in \mathfrak{S}_k}{\mathrm{sgn}}(\sigma)g^{\mu_1\nu_{\sigma(1)}}\dots g^{\mu_k\nu_{\sigma(k)}}\\ &= \frac{1}{(k!)^2}\sum_{\sigma\in \mathfrak{S}_k} \alpha_{\mu_1\dots\mu_k}\beta_{\nu_1\dots\nu_k}{\mathrm{sgn}}(\sigma)g^{\mu_1\nu_{\sigma(1)}}\dots g^{\mu_k\nu_{\sigma(k)}}\\ &=\frac{1}{(k!)^2}\sum_{\sigma\in \mathfrak{S}_k}{\mathrm{sgn}}(\sigma) \alpha^{\nu_{\sigma(1)}\dots\nu_{\sigma(k)}}\beta_{\nu_1\dots\nu_k}\\ &=\frac{1}{(k!)^2}\sum_{\sigma\in \mathfrak{S}_k}\alpha^{\nu_{1}\dots\nu_{k}}\beta_{\nu_1\dots\nu_k}\\ &=\frac{1}{k!}\alpha^{\nu_{1}\dots\nu_{k}}\beta_{\nu_1\dots\nu_k}. \end{aligned}\]

Here we used the fact that the components of a form are totally antisymmetric, so for any permutation $\sigma\in \mathfrak{S}_k$

\[\alpha_{\mu_{\sigma(1)}\dots\mu_{\sigma(k)}}={\mathrm{sgn}}(\sigma)\alpha_{\mu_1\dots\mu_k}.\]

With this result we can see that $g:\Lambda^kV\times\Lambda^kV\to {\mathbb{R}}$ is non-degenerate. Choose an orthonormal basis $e^1,\dots,e^n$ of $V$. Then we have

\[g(e^{\mu_1}\wedge\dots\wedge e^{\mu_k},e^{\nu_1}\wedge\dots\wedge e^{\nu_k}) = \sum_{\sigma\in \mathfrak{S}_k}{\mathrm{sgn}}(\sigma)g^{\mu_1\nu_{\sigma(1)}}\dots g^{\mu_k\nu_{\sigma(k)}}.\]

However, since the basis is orthonormal then $g^{ii}=\pm 1$ and $g^{ij}=0$ if $i\neq j$. From this we see that if $\{\mu_1,\dots,\mu_k\}\neq \{\nu_1,\dots,\nu_k\}$, then for absolutely no permutation $\sigma\in \mathfrak{S}_k$ we will have $\mu_1=\nu_{\sigma(1)}$ and $\dots$ and $\mu_k=\nu_{\sigma(k)}$. Thus the inner product is nonzero only if $\{\mu_1,\dots,\mu_k\}=\{\nu_1,\dots,\nu_k\}$. In this case, then, we have that $(\mu_1,\dots,\mu_k)$ is precisely a permutation of $(\nu_1,\dots,\nu_k)$. Since all symbols $\mu_1,\dots,\mu_k$ must be distinct (otherwise $e^{\mu_1}\wedge\dots\wedge e^{\mu_k}$ is zero to begin with), we then have that there is only one permutation that survives in the sum, the one for which precisely $\nu_{\sigma(i)}=\mu_i$. In conclusion:

\[g(e^{\mu_1}\wedge\dots\wedge e^{\mu_k},e^{\nu_1}\wedge\dots\wedge e^{\nu_k}) = \begin{cases} (-1)^s{\mathrm{sgn}}(\sigma) & \text{if there exists }\sigma\text{ such that }\nu_{\sigma(j)}=\mu_j\\ 0 &\text{ otherwise} \end{cases},\]

where here $s$ is the number the number of elements in $\{e^{\mu_1},\dots,e^{\mu_k}\}$ which have negative length. Since we know that the elements of the form $e^{\mu_1}\wedge\dots\wedge e^{\mu_k}$ form a basis for $\Lambda^kV$, the previous result tells us that in this basis the matrix of $g$ is diagonal with entries $\pm 1$, and thus $g$ is non-degenerate.

Defining the Hodge star

Now let ${\mathrm{vol}}\in \Lambda^nV$ be a volume form on $V$, given in terms of an oriented orthonormal basis $e_1,\dots,e_n$ as

\[{\mathrm{vol}}= e_1\wedge\dots\wedge e_n.\]

We now define the Hodge star operator $\star:\Lambda^kV\to \Lambda^{n-k}V$, as the unique linear operator such that for all $\alpha,\beta\in \Lambda^{k}V$,

\[\alpha\wedge\star\beta = g(\alpha,\beta){\mathrm{vol}}.\]

Here we’ve sneakily claimed that such a linear operator exists and is unique. We need to prove that. First, for each $\beta\in \Lambda^{n-k}V$ define a map $\phi_\beta:\Lambda^{k}V\to {\mathbb{R}}$ such that

\[\alpha\wedge\beta =\phi_{\beta}(\alpha){\mathrm{vol}}.\]

This map is well-defined and clearly linear, i.e. $\phi_\beta\in (\Lambda^{k}V)^*$. In particular, we can see that in components with respect to an orthonormal basis $e^1,\dots,e^n$ of $V$,

\[\alpha\wedge\beta = \frac{1}{k!(n-k)!}\alpha_{\mu_1\dots\mu_k}\beta_{\nu_1\dots\nu_{n-k}}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}}{\mathrm{vol}},\]

where $\epsilon^{\lambda_1\dots\lambda_n}$ is the Levi-Civita symbol, so that

\[\phi_\beta(\alpha) = \frac{1}{k!(n-k)!}\alpha_{\mu_1\dots\mu_k}\beta_{\nu_1\dots\nu_{n-k}}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}}.\]

Now let’s see that the assignment, let’s call it $\phi:\Lambda^{n-k}V\to (\Lambda^kV)^*$, given as $\beta\mapsto \phi_\beta$ is an isomorphism. First, it is clearly linear. Now suppose that $\phi_\beta=0$, i.e. for all $\alpha\in\Lambda^{k}V$, $\phi_\beta(\alpha)=0$. In particular, for $\alpha=e^{\rho_1}\wedge\dots\wedge e^{\rho_k}$,

\[0 = \phi_\beta(e^{\rho_1}\wedge\dots\wedge e^{\rho_k}) = \frac{1}{k!(n-k)!}(e^{\rho_1}\wedge\dots\wedge e^{\rho_k})_{\mu_1\dots\mu_k}\beta_{\nu_1\dots\nu_{n-k}}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}}.\]

Now we have that the components of the basis itself are

\[(e^{\rho_1}\wedge\dots\wedge e^{\rho_k})_{\mu_1\dots\mu_k} = \begin{cases} 0 &\text{if }{\left\{\mu_1,\dots,\mu_k\right\}}\neq {\left\{\rho_1,\dots,\rho_k\right\}}\\ {\mathrm{sgn}}(\sigma) &\text{ if }\sigma\in \mathfrak{S}_k\text{ such that }\rho_i=\mu_{\sigma(i)} \end{cases}.\]

We denote the right-hand side as the following symbol:

\[\delta^{\rho_1\dots\rho_k}_{\mu_1\dots\mu_k}:= \begin{cases} 0 &\text{if }{\left\{\mu_1,\dots,\mu_k\right\}}\neq {\left\{\rho_1,\dots,\rho_k\right\}}\\ {\mathrm{sgn}}(\sigma) &\text{ if }\sigma\in \mathfrak{S}_k\text{ such that }\rho_i=\mu_{\sigma(i)} \end{cases}.\]

A little bit of tedious work shows that

\[\delta^{\rho_1\dots\rho_k}_{\mu_1\dots\mu_k} = \det([\delta^{\rho_i}_{\mu_j}]),\]

i.e. the determinant of the matrix whose $(i,j)$-th entry is $\delta^{\rho_i}_{\mu_j}$. Now when we plug this back in, we get

\[0 = \phi_\beta(e^{\rho_1}\wedge\dots\wedge e^{\rho_k}) = \frac{1}{k!(n-k)!}\delta^{\rho_1\dots\rho_k}_{\mu_1\dots\mu_k}\beta_{\nu_1\dots\nu_{n-k}}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}}.\]

Here we are implicitly summing over all the $\mu_i$ indices. From the definition above, the only terms that survive in the sum are those for which there exists a permutation $\sigma\in\mathfrak{S}_k$ such that $\mu_i=\rho_{\sigma(i)}$. Therefore,

\[\begin{aligned} \phi_\beta(e^{\rho_1}\wedge\dots\wedge e^{\rho_k}) &= \frac{1}{k!(n-k)!}\sum_{\sigma\in \mathfrak{S}_k}\beta_{\nu_1\dots \nu_{n-k}}{\mathrm{sgn}}(\sigma)\epsilon^{\rho_{\sigma(1)}\dots\rho_{\sigma(k)}\nu_1\dots\nu_{n-k}}\\ &=\frac{1}{k!(n-k)!}\sum_{\sigma\in \mathfrak{S}_k}\beta_{\nu_1\dots \nu_{n-k}}\epsilon^{\rho_{1}\dots\rho_{k}\nu_1\dots\nu_{n-k}}\\ &=\frac{1}{(n-k)!}\beta_{\nu_1\dots \nu_{n-k}}\epsilon^{\rho_{1}\dots\rho_{k}\nu_1\dots\nu_{n-k}} \end{aligned}\]

For each set of indices ${\{\nu_1,\dots,\nu_{n-k}\}}$ if we choose ${\{\rho_1,\dots,\rho_{k}\}}$ complementary to ${\{\nu_1,\dots,\nu_{n-k}\}}$ in ${\{1,\dots,n\}}$, then we have that $\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}=\pm 1$ and so $\beta_{\nu_1\dots\nu_{n-k}}=0$. Therefore $\beta=0$. The map $\phi:\beta\mapsto \phi_\beta$ is injective, then, and since $\dim(\Lambda^{n-k}V)=\dim(\Lambda^{k}V)=\dim((\Lambda^{k}V)^*)$, we obtain that it is an isomorphism.

Recall that we have a metric $g$ on $\Lambda^k V$, which induces an isomorphism $g_\flat:\Lambda^kV\mapsto (\Lambda^kV)^*$, given as $g_{\flat}(\alpha):=g(\cdot,\alpha)$. We define then $\star:\Lambda^kV\to \Lambda^{n-k}V$ as $\star\alpha$ being the unique element in $\Lambda^{n-k}V$ such that

\[\phi_{\star \alpha}=g_{\flat}(\alpha).\]

If you want to, you could write $\star=\phi^{-1}\circ g_{\flat}$. At once, this tells us that for any $\alpha,\beta\in \Lambda^{k}V$,

\[\alpha\wedge\star\beta = \phi_{\star\beta}(\alpha){\mathrm{vol}}= g_\flat(\beta)(\alpha){\mathrm{vol}}= g(\alpha,\beta){\mathrm{vol}}.\]

Okay so the map exists. What about uniqueness? Suppose there is an isomorphism $\xi:\Lambda^kV\to\Lambda^{n-k}V$ such that $\alpha\wedge\xi(\beta)=g(\alpha,\beta){\mathrm{vol}}$. This tells us that $\phi_{\xi(\beta)}(\alpha)=g(\alpha,\beta)$, i.e. that $\phi_{\xi(\beta)}=g_\flat(\beta)$. But then, by our definition of $\star$, this precisely means that $\xi(\beta)=\star\beta$.

Now a quick example which will help us down the road: We want to compute $\star(e^{\rho_1}\wedge\dots\wedge e^{\rho_k})$. We use the fact that $\star$ is an isomorphism, so we can make an educated guess and just check it works. Whatever it is, it has to satisfy

\[(e^{\rho_1}\wedge\dots\wedge e^{\rho_k})\wedge \star(e^{\rho_1}\wedge\dots\wedge e^{\rho_k}) = g(e^{\rho_1}\wedge\dots\wedge e^{\rho_k},e^{\rho_1}\wedge\dots\wedge e^{\rho_k}){\mathrm{vol}}= (-1)^s{\mathrm{vol}},\]

where $s$ is, again, the number of negative eigenvalues of the metric. This means that $\star(e^{\rho_1}\wedge\dots\wedge e^{\rho_k})$ has to consist of the wedges of the basis elements that we don’t have in $e^{\rho_1},\dots,e^{\rho_k}$. That is, let ${\{\nu_1,\dots,\nu_{n-k}\}}$ be complementary to ${\{\rho_1,\dots,\rho_k\}}$ in ${\{1,\dots,n\}}$. Therefore,

\[e^{\rho_1}\wedge\dots\wedge e^{\rho_k}\wedge e^{\nu_1}\wedge\dots\wedge e^{\nu_{n-k}} = \epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}{\mathrm{vol}}.\]

With this, we then see that

\[\star(e^{\rho_1}\wedge\dots\wedge e^{\rho_k}) = (-1)^s\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}(e^{\nu_1}\wedge\dots\wedge e^{\nu_{n-k}}) \qquad\text{(no Einstein sum)}.\]

Making it useful: formulas in coordinates

This is all nice and all but we want to compute the star of a form explicitly if we have it in terms of some basis. Can do! Let $e^1,\dots,e^n$ be an orthonormal basis of $V$. By definition, we have for any $\alpha,\beta\in \Lambda^k V$, that

\[\alpha\wedge\star\beta = g(\alpha,\beta){\mathrm{vol}}.\]

In components with respect to the orthonormal basis, this is

\[\frac{1}{k!(n-k)!}\alpha_{\mu_1\dots\mu_k}(\star\beta)_{\nu_1\dots\nu_{n-k}}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}} = \frac{1}{k!}\alpha^{\mu_1\dots\mu_k}\beta_{\mu_1\dots\mu_k}.\]

Again, we choose $\alpha=e^{\rho_1}\wedge\dots\wedge e^{\rho_k}$, so that we obtain

\[\frac{1}{k!(n-k)!}\delta^{\rho_1\dots\rho_k}_{\mu_1\dots\mu_k}(\star\beta)_{\nu_1\dots\nu_{n-k}}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}} = \frac{1}{k!}g^{\mu_1\lambda_1}\dots g^{\mu_k \lambda_k}\delta_{\lambda_1\dots\lambda_k}^{\rho_1\dots\rho_k}\beta_{\mu_1\dots\mu_k}.\]

On the right-hand side, we have

\[g^{\mu_1\lambda_1}\dots g^{\mu_k \lambda_k}\delta_{\lambda_1\dots\lambda_k}^{\rho_1\dots\rho_k}\beta_{\mu_1\dots\mu_k} = \delta_{\lambda_1\dots\lambda_k}^{\rho_1\dots\rho_k}\beta^{\lambda_1\dots\lambda_k}.\]

But now recall that $\delta_{\lambda_1\dots\lambda_k}^{\rho_1\dots\rho_k}$ is non-zero only when there is a permutation $\sigma$ such that $\lambda_i=\rho_{\sigma(i)}$. Then we have

\[\delta_{\lambda_1\dots\lambda_k}^{\rho_1\dots\rho_k}\beta^{\lambda_1\dots\lambda_k} = \sum_{\sigma\in \mathfrak{S}_k}\delta_{\rho_{\sigma(1)}\dots\rho_{\sigma(k)}}^{\rho_1\dots\rho_k}\beta^{\rho_{\sigma(1)}\dots\rho_{\sigma(k)}} = \sum_{\sigma\in \mathfrak{S}_k}{\mathrm{sgn}}(\sigma)\beta^{\rho_{\sigma(1)}\dots\rho_{\sigma(k)}}= \sum_{\sigma\in \mathfrak{S}_k}{\mathrm{sgn}}(\sigma)^2\beta^{\rho_{1}\dots\rho_{k}}=k!\beta^{\rho_1\dots\rho_k}.\]

On the left-hand side, we have something similar:

\[\delta^{\rho_1\dots\rho_k}_{\mu_1\dots\mu_k}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}} = k!\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}.\]

When we put it all together, we get

\[\frac{1}{(n-k)!}(\star\beta)_{\nu_1\dots\nu_{n-k}}\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}=\beta^{\rho_1\dots\rho_{k}}.\]

We are nearly done! We only need to get rid of that Levi-Civita symbol on the left-hand side. To do so, consider the sum¹

\[\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}\epsilon_{\rho_1\dots\rho_k\lambda_1\dots\lambda_{n-k}}.\]

The only terms of the sum that are non-zero are when ${\{\rho_1,\dots,\rho_k\}}$ is complementary to both the sets ${\{\nu_1,\dots,\nu_{n-k}\}}$ and ${\{\lambda_1,\dots,\lambda_{n-k}\}}$ in ${\{1,\dots,n\}}$. This implies that the sum is non-zero only if ${\{\lambda_1,\dots,\lambda_{n-k}\}}={\{\nu_1,\dots,\nu_{n-k}\}}$. Then suppose that there is some $\sigma\in\mathfrak{S}{n-k}$ such that $\lambda_i=\nu{\sigma(i)}$. Without the Einstein convention, this becomes:

\[\begin{aligned} \sum_{\rho_1,\dots,\rho_k}\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}\epsilon_{\rho_1\dots\rho_k\nu_{\sigma(1)}\dots\nu_{\sigma(n-k)}} &= \sum_{\rho_1,\dots,\rho_k}{\mathrm{sgn}}(\sigma)\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}\epsilon_{\rho_1\dots\rho_k\nu_{1}\dots\nu_{n-k}}\\ &= \sum_{\rho_1,\dots,\rho_k}{\mathrm{sgn}}(\sigma)(\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}})^2\\ &=\sum_{\rho_1,\dots,\rho_k}{\mathrm{sgn}}(\sigma)(\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}})^2\\ &=k!{\mathrm{sgn}}(\sigma). \end{aligned}\]

In conclusion, we have that

\[\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}\epsilon_{\rho_1\dots\rho_k\lambda_1\dots\lambda_{n-k}} = k!\delta^{\nu_1\dots\nu_{n-k}}_{\lambda_1\dots\lambda_{n-k}}.\]

With this, finally we obtain

\[\frac{1}{(n-k)!}(\star\beta)_{\nu_1\dots\nu_{n-k}}\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}\epsilon_{\rho_1\dots\rho_k\lambda_1\dots\lambda_{n-k}} = \frac{k!}{(n-k)!}(\star\beta)_{\nu_1\dots\nu_{n-k}}\delta^{\nu_1\dots\nu_{n-k}}_{\lambda_1\dots\lambda_{n-k}} = k!(\star\beta)_{\lambda_1\dots\lambda_{n-k}}.\]

Now we put it all together:

\[k!(\star\beta)_{\lambda_1\dots\lambda_{n-k}} =\beta^{\rho_1\dots\rho_k}\epsilon_{\rho_1\dots\rho_k\lambda_1\dots\lambda_{n-k}},\]

i.e.

\[(\star\beta)_{\lambda_1\dots\lambda_{n-k}}=\frac{1}{k!}\beta^{\rho_1\dots\rho_k}\epsilon_{\rho_1\dots\rho_k\lambda_1\dots\lambda_{n-k}}.\]

And we’re done! Right? We’re done, right? … guys? What’s wrong?

…

What do you mean you want it for a general basis?

Okay let $u^1,\dots,u^n$ be some basis, and let $A$ be the change-of-basis matrix from the $e$ to the $u$ basis, such that

\[u^i = A^{i}_{\phantom{i}j}e^j.\]

In this new basis, the volume form is not $u^1\wedge\dots\wedge u^n$, but these two are non-zero top-forms so they’re only scalar multiples of one another. Explicitly,

\[u^1\wedge\dots\wedge u^n = A^1_{\phantom{1}\mu_1}\dots A^n_{\phantom{n}\mu_n}e^{\mu_1}\wedge\dots\wedge e^{\mu_n} = A^1_{\phantom{1}\mu_1}\dots A^n_{\phantom{n}\mu_n}\epsilon^{\mu_1\dots\mu_n}e^{1}\wedge\dots\wedge e^{n} = \det(A){\mathrm{vol}}.\]

What is $\det(A)$? Fortunately we can calculate it easily: Let $g_{u}$ be the matrix representation of $g$ on the $u$-basis, namely

\[[g_u]^{\mu\nu}=g(u^\mu,u^{\nu}).\]

Then

\[[g_u]^{\mu\nu}=g(u^\mu,u^{\nu}) = A^{\mu}_{\phantom{\mu}\rho}A^{\nu}_{\phantom{\nu}\lambda}g(e^{\rho},e^\lambda) = A^{\mu}_{\phantom{\mu}\rho}[g_e]^{\rho\lambda}A^{\nu}_{\phantom{\nu}\lambda}=[A\cdot g_e\cdot A^T]^{\mu\nu},\]

where $g_e$ is the matrix representation of $g$ with respect to the orthonormal basis, i.e. $g_e$ is diagonal with $\pm 1$ on the diagonal. Taking the determinant we get

\[\det(g_u)= \det(A)^2\det(g_e)=(-1)^s\det(A)^2,\]

with $s$ being the number of negative eigenvalues of $g_e$ (also known as the signature of the metric). Thus,

\[\det(A) = \pm\sqrt{|\det(g_u)|},\]

where the sign depends on the orientation of the $u$ basis. Thus,

\[u^1\wedge\dots\wedge u^n = \pm \sqrt{|\det(g_u)|}{\mathrm{vol}}.\]

With this we can find the expression for $\star$ with respect to any choice of basis. In the $u$ basis, we have

\[\begin{aligned} \alpha\wedge\star\beta&=\frac{1}{k!(n-k)!}\alpha_{\mu_1\dots\mu_k}(\star\beta)_{\nu_1\dots\nu_{n-k}}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}}u^1\wedge\dots\wedge u^n\\ &=\frac{\pm\sqrt{|\det{g_u}|}}{k!(n-k)!}\alpha_{\mu_1\dots\mu_k}(\star\beta)_{\nu_1\dots\nu_{n-k}}\epsilon^{\mu_1\dots\mu_k\nu_1\dots\nu_{n-k}}{\mathrm{vol}}. \end{aligned}\]

And thus we can repeat the same process as we did above, just that we need to carry the $\pm\sqrt{|\det(g_u)|}$ on the left-hand side for the whole ride. In the end, we get

\[(\star\beta)_{\lambda_1\dots\lambda_{n-k}}=\pm\frac{1}{k!}\frac{1}{\sqrt{|\det(g_u)|}}\beta^{\rho_1\dots\rho_k}\epsilon_{\rho_1\dots\rho_k\lambda_1\dots\lambda_{n-k}}.\]

Alright before you say anything, yes, I know that this is not the same equation that you’ll see basically everywhere else; the determinant of the metric should in the numerator, you say? Yes, but actually no. See, here we worked with the exterior algebra of a vector space $V$, not its dual. In practice, with differential forms, we’re working with the exterior algebra of differential forms, which are dual to the tangent spaces. That changes the formula a little bit since the matrix of the metric on the dual is the inverse of the matrix in the tangent space.

On differential forms

Before jumping head-first to differential forms, let’s see what happens when we try to apply all this on the dual. If we have a metric $g$ on $V$, it induces isomorphisms $g_{\flat}:V\to V^*$ and $g^{\sharp}=(g_{\flat})^{-1}:V^*\to V$, given as

\[g_\flat(v)(u)=g(v,u)\]

for all $u, v\in V$, and similarly, for all $\alpha\in V^*$, we have that $g^\sharp(\alpha)\in V$ is such that

\[g(g^\sharp(\alpha),u)=\alpha(u)\]

for all $u\in V$. If we take a basis (INDEX SWITCH ALERT) $u_1,\dots,u_k\in V$, and write $v=v^\mu u_\mu$, then what are the components of $g_\flat(v)$? If $u^1,\dots,u^k$ is the dual basis of $V^*$, then we can write

\[g_\flat(v)=(g_\flat(v))_\mu u^\mu,\]

where

\[g_\flat(v)_\mu = g_\flat(v)(u_\mu)=g(v,u_\mu)=v^\nu g(u_\nu,u_\mu):=v^\nu g_{\nu\mu}.\]

Here we write $g_{\mu\nu}=g(u_\mu,u_\nu)$ as the components of the metric in this basis. We call this lowering the index of $v$, and we simply abuse notation by writing $g_\flat(v)=v_\mu u^\mu$, with $v_\mu:=v^\nu g_{\nu\mu}$.

Similarly, if $\alpha=\alpha_\mu u^\mu\in V^*$, then we have that

\[\alpha_\nu=\alpha(e_\nu)=g(g^\sharp(\alpha),e_\nu)=(g^\sharp(\alpha))^\mu g(u_{\mu},u_\nu)=(g^\sharp(\alpha))^\mu g_{\mu\nu}.\]

Thus we can invert this matrix equation and write

\[(g^\sharp(\alpha))^\mu := (g^{-1})^{\mu\nu}\alpha_\nu,\]

where $(g^{-1})^{\mu\nu}$ are the components² of the inverse of the matrix of $g$.

So far so good. Now we can simply pull back the metric $g$ from $V$ to $V^*$ using $g^\sharp$, and define (using the same symbol), for any $\alpha,\beta\in V^*$,

\[g(\alpha,\beta)=g(g^\sharp(\alpha),g^{\sharp}(\beta)).\]

What are the components of the dual metric with respect to the $u^1,\dots,u^n$ basis? Well we compute

\[\begin{aligned} g^{\mu\nu}=g(e^\mu,e^\nu)=g(g^\sharp(e^\mu),g^\sharp(e^{\nu}))&=(g^{-1})^{\alpha\beta}(g^{-1})^{\rho\sigma}g((e^\mu)_{\beta}e_\alpha,(e^\nu)_\sigma e_\rho)\\ &= (g^{-1})^{\alpha\mu}(g^{-1})^{\rho\nu}g(e_\alpha,e_\rho)\\ &=(g^{-1})^{\alpha\mu}(g^{-1})^{\rho\nu}g_{\alpha\rho}\\ &= (g^{-1})^{\mu\nu}.\end{aligned}\]

Thus the components of the metric on $V^*$ are the components of the inverse of the metric on $V$. We drop the clunky $^{-1}$ from now on since there is no ambiguity: $g^{\mu\nu}$ always means the components of the inverse of the matrix with entries $g_{\mu\nu}$.

Now we’re done! Let $M$ be a smooth manifold with a Lorentzian metric $g$. We will apply all this, pointwise, to the cotangent spaces of $M$. By definition, $g$ is a smooth tensor field on $M$ which is point-wise a metric $g_x:T_xM\times T_xM\to {\mathbb{R}}$. This metric induces a metric $g^{\text{dual}}$ on $T_x^*M$ via the isomorphism $(g_x)^\sharp:T_x^*M\to T_xM$ as above. Now we define the Hodge-dual pointwise but on the cotangent space, so the metric we use is the inverse of the metric on $TM$. That is, in the notation of section Defining the Hodge star we let $V=T_x^*M$, so that the Hodge star is $\star:\Omega_x^k(M)\to\Omega_x^{n-k}(M)$, but in this case the components are

\[(\star\beta)_{\lambda_1\dots\lambda_{n-k}}=\pm\frac{1}{k!}\frac{1}{\sqrt{|\det(g^\text{dual}_u)|}}\beta^{\rho_1\dots\rho_k}\epsilon_{\rho_1\dots\rho_k\lambda_1\dots\lambda_{n-k}} = \pm\frac{\sqrt{|\det(g_u)|}}{k!}\beta^{\rho_1\dots\rho_k}\epsilon_{\rho_1\dots\rho_k\lambda_1\dots\lambda_{n-k}}.\]

If you look at this expression, it is obviously smooth since the components of $g$ and $\beta$ are and $\det(g_u)$ is non-zero. Thus we can happily extend $\star$ to be a global operator

\[\star:\Omega^k(M)\to \Omega^{n-k}(M).\]

A neat example: de Rham vs. curl, grad, div

Now let’s make it explicit. We consider $M={\mathbb{R}}^3$, with its natural euclidean metric $g$, and coordinates $x,y,z$. The volume form is simply

\[{\mathrm{vol}}= {\mathrm{d}}{x}\wedge{\mathrm{d}}{y}\wedge{\mathrm{d}}{z}.\]

Now let’s see what $\star$ does to $0$, $1$, $2$, and $3$-forms. First, recall that if $e^1,\dots,e^n$ is an orthonormal basis, then

\[\star(e^{\rho_1}\wedge\dots\wedge e^{\rho_k}) = (-1)^s\epsilon^{\rho_1\dots\rho_k\nu_1\dots\nu_{n-k}}(e^{\nu_1}\wedge\dots\wedge e^{\nu_{n-k}}) \qquad\text{(no Einstein sum)},\]

where $s$ is the number of elements in $\{e^{\rho_1},\dots,e^{\rho_k}\}$ with negative length, and ${\{\nu_1,\dots,\nu_{n-k}\}}$ is complementary to ${\{\rho_1,\dots,\rho_k\}}$ in ${\{1,\dots,n\}}$. Now a $0$-form is just a smooth function, say $f$, and we simply have

\[\star f =f{\mathrm{vol}}= f(x,y,z){\mathrm{d}}{x}\wedge{\mathrm{d}}{y}\wedge{\mathrm{d}}{z}.\]

Now for one-forms, the above result tells us that

\[\begin{aligned} \star({\mathrm{d}}{x}) &= {\mathrm{d}}{y}\wedge{\mathrm{d}}{z}\\ \star({\mathrm{d}}{y}) &= {\mathrm{d}}{z}\wedge{\mathrm{d}}{x}\\ \star({\mathrm{d}}{z}) &= {\mathrm{d}}{x}\wedge{\mathrm{d}}{y}, \end{aligned}\]

so that

\[\star(\omega_x{\mathrm{d}}{x}+\omega_y{\mathrm{d}}{y}+\omega_z{\mathrm{d}}{z})=\omega_x{\mathrm{d}}{y}\wedge{\mathrm{d}}{z} + \omega_y{\mathrm{d}}{z}\wedge{\mathrm{d}}{x}+\omega_z{\mathrm{d}}{x}\wedge{\mathrm{d}}{y}.\]

Similarly, for $2$-forms we have

\[\star(\omega_{yz}{\mathrm{d}}{y}\wedge{\mathrm{d}}{z} + \omega_{zx}{\mathrm{d}}{z}\wedge{\mathrm{d}}{x}+\omega_{xy}{\mathrm{d}}{x}\wedge{\mathrm{d}}{y})=\omega_{yz}{\mathrm{d}}{x}+\omega_{zx}{\mathrm{d}}{y}+\omega_{xy}{\mathrm{d}}{z}.\]

For $3$-forms, \(\star(f{\mathrm{vol}}) = f.\)

Now let’s talk about grad, curl, and div. Just as a reminder and for the sake of completeness, let’s write them down. Let $U\subseteq M$ be an open set. Then we define ${\mathrm{grad}}:C^{\infty}(U)\to \mathfrak{X}(U)$ as

\[{\mathrm{grad}}(f) = {\frac{\partial f}{\partial x}}{\frac{\partial }{\partial x}} + {\frac{\partial f}{\partial y}}{\frac{\partial }{\partial y}} + {\frac{\partial f}{\partial z}}{\frac{\partial }{\partial z}} = g^\sharp({\mathrm{d}}{f}).\]

We define ${\mathrm{curl}}:\mathfrak{X}(U)\to \mathfrak{X}(U)$, defined as

\[{\mathrm{curl}}\left(f^x{\frac{\partial }{\partial x}} + f^y{\frac{\partial }{\partial y}} + f^z{\frac{\partial }{\partial z}}\right) = \left({\frac{\partial f^z}{\partial y}} - {\frac{\partial f^y}{\partial z}}\right){\frac{\partial }{\partial x}} + \left({\frac{\partial f^x}{\partial z}} - {\frac{\partial f^z}{\partial x}}\right){\frac{\partial }{\partial y}} + \left({\frac{\partial f^y}{\partial x}} - {\frac{\partial f^y}{\partial x}}\right){\frac{\partial }{\partial z}},\]

and finally, ${\mathrm{div}}:\mathfrak{X}(U)\to C^{\infty}(U)$ given as

\[{\mathrm{div}}\left(f^x{\frac{\partial }{\partial x}} + f^y{\frac{\partial }{\partial y}} + f^z{\frac{\partial }{\partial z}}\right) = {\frac{\partial f^x}{\partial x}} + {\frac{\partial f^y}{\partial y}} + {\frac{\partial f^z}{\partial z}}.\]

It is an elementary exercise to prove that ${\mathrm{curl}}\circ {\mathrm{grad}}= 0$ and ${\mathrm{div}}\circ {\mathrm{curl}}= 0$, so that we have a complex

\[0 \to C^\infty(U)\overset{\mathrm{grad}}{\to}\mathfrak{X}(U)\overset{\mathrm{curl}}{\to}\mathfrak{X}(U)\overset{\mathrm{div}}{\to} C^\infty(U)\to 0,\]

called the gcd complex.

Now let’s compare this to the de Rham differential, explicitly to be more clear: for a $0$-form,

\[{\mathrm{d}}f = {\frac{\partial f}{\partial x}}{\mathrm{d}}{x} + {\frac{\partial f}{\partial y}}{\mathrm{d}}{y} + {\frac{\partial f}{\partial z}}{\mathrm{d}}{z}.\]

For a $1$-form,

\[{\mathrm{d}}(\omega_x{\mathrm{d}}{x}+\omega_y{\mathrm{d}}{y}+\omega_z{\mathrm{d}}{z})=\left({\frac{\partial \omega_z}{\partial y}}-{\frac{\partial \omega_y}{\partial z}}\right){\mathrm{d}}{y}\wedge{\mathrm{d}}{z} + \left({\frac{\partial \omega_x}{\partial z}}-{\frac{\partial \omega_z}{\partial x}}\right){\mathrm{d}}{z}\wedge{\mathrm{d}}{x} + \left({\frac{\partial \omega_y}{\partial x}}-{\frac{\partial \omega_x}{\partial y}}\right){\mathrm{d}}{x}\wedge{\mathrm{d}}{y}.\]

And for a $2$-form,

\[{\mathrm{d}}(\omega_{yz}{\mathrm{d}}{y}\wedge{\mathrm{d}}{z} + \omega_{zx}{\mathrm{d}}{z}\wedge{\mathrm{d}}{x}+\omega_{xy}{\mathrm{d}}{x}\wedge{\mathrm{d}}{y}) = \left({\frac{\partial \omega_{yz}}{\partial x}} + {\frac{\partial \omega_{zx}}{\partial y}} +{\frac{\partial \omega_{xy}}{\partial z}}\right){\mathrm{d}}{x}\wedge{\mathrm{d}}{y}\wedge{\mathrm{d}}{z}.\]

This tells us that there is an isomorphism between the gcd complex and the de Rham complex, given as $\phi_0:C^\infty(U)\to C^\infty(U)$ being simply $\phi_0={\mathrm{id}}$. We also have $\phi_1:\mathfrak{X}(U)\to \Omega^1(U)$ as

\[\phi_1\left(f^x{\frac{\partial }{\partial x}} + f^y{\frac{\partial }{\partial y}} + f^z{\frac{\partial }{\partial z}}\right) = f^x{\mathrm{d}}{x} + f^y{\mathrm{d}}{y} + f^z{\mathrm{d}}{z},\]

i.e. $\phi_1=g_\flat$. We also have $\phi_2:\mathfrak{X}(U)\to\Omega^2(U)$ given as

\[\phi_2\left(f^x{\frac{\partial }{\partial x}} + f^y{\frac{\partial }{\partial y}} + f^z{\frac{\partial }{\partial z}}\right) = f^x{\mathrm{d}}{y}\wedge{\mathrm{d}}{z} + f^y{\mathrm{d}}{z}\wedge{\mathrm{d}}{x}+f^z{\mathrm{d}}{x}\wedge{\mathrm{d}}{y},\]

which we can identify as $\phi_2 = \star\circ g_\flat$. Finally, we have $\phi_3:C^{\infty}(U)\to\Omega^3(U)$ given as

\[\phi_3(f)=f{\mathrm{d}}{x}\wedge{\mathrm{d}}{y}\wedge{\mathrm{d}}{z}=\star(f).\]

By construction, we have $\phi_0=\mathrm{id}_{C^{\infty}(U)}$, $\phi_1=g_\flat$, $\phi_2=\star\circ g_{\flat}$ and $\phi_3=\star$, all of which are isomorphisms. Now we need to check that the diagram

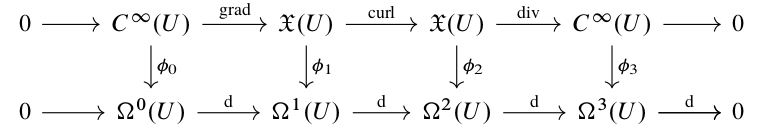
commutes… but this is a straightforward, albeit a bit boring, computation. Therefore we have that $\phi_\bullet$ is an isomorphism of complexes, which induces an isomorphism in cohomology:

\[\begin{aligned} \ker({\mathrm{grad}})&\cong H^0(U)\\ \ker({\mathrm{curl}})/{\mathrm{im}}({\mathrm{grad}})&\cong H^1(U)\\ \ker({\mathrm{div}})/{\mathrm{im}}({\mathrm{curl}})&\cong H^2(U)\\ C^\infty(U)/{\mathrm{im}}({\mathrm{div}}) &\cong H^3(U).\end{aligned}\]

So suppose you have a vector field $\mathbf{E}\in \mathfrak{X}(U)$ satisfying ${\mathrm{curl}}(\mathbf{E})=0$. When can you guarantee that $\mathbf{E}={\mathrm{grad}}({\varphi})$ for some scalar function ${\varphi}\in C^\infty(U)$? The previous result tells us that when $H^1(U)=0$, i.e. when $U$ is simply connected, then every irrotational field is a gradient. Similarly, if you have a field $\mathbf{B}$ such that ${\mathrm{div}}(\mathbf{B})=0$, then if $H^2(U)=0$, we can guarantee that $\mathbf{B}={\mathrm{curl}}(\mathbf{A})$ for some field $\mathbf{A}\in \mathfrak{X}(U)$.

Another neat example: wedge and cross product

Have you noticed that the cross product in ${\mathbb{R}}^3$ behaves very similarly to the wedge product? With the antisymmetry and all. There is, of course, a huge difference between both: the cross product returns another vector in ${\mathbb{R}}^3$, i.e. $\times:{\mathbb{R}}^3\times{\mathbb{R}}^3\to {\mathbb{R}}^3$, whereas the wedge product returns an element of the exterior product of ${\mathbb{R}}^3$ with itself, $\wedge:{\mathbb{R}}^3\times {\mathbb{R}}^3\to {\mathbb{R}}^3\wedge{\mathbb{R}}^3$. How can we bridge both?

On ${\mathbb{R}}^3$ we have the canonical euclidean metric $g$, and thus we have the Hodge star $\star:{\mathbb{R}}^3\wedge{\mathbb{R}}^3\to {\mathbb{R}}^3$. With this we can construct an antisymmetric map $\star\circ\wedge:{\mathbb{R}}^3\times{\mathbb{R}}^3\to {\mathbb{R}}^3$.

Let $e_1,e_2,e_3$ be the canonical orthonormal basis of ${\mathbb{R}}^3$. We then see that

\[\begin{aligned} \star(e_1\wedge e_2)&=e_3\\ \star(e_2\wedge e_3)&=e_1\\ \star(e_3\wedge e_1)&=e_2.\end{aligned}\]

However, this is the same as

\[\begin{aligned} e_1\times e_2&=e_3\\ e_2\times e_3&=e_1\\ e_3\times e_1&=e_2.\end{aligned}\]

We then happily conclude that

\[u\times v = \star(u\wedge v)\]

for all $u,v\in {\mathbb{R}}^3$.

The takeaway

The Hodge star operator makes an explicit isomorphism between the exterior powers $\Lambda^kV$ and $\Lambda^{n-k}V$ of a vector space with the aid of a metric. With it we can bridge the similarities between exterior products of complementary degrees. It also makes explicit the relationship between the cross product and vector calculus in ${\mathbb{R}}^3$ and the calculus and algebra of differential forms on it. As a quick corollary, we saw that the existence of potentials for certain functions depends on the topology of the underlying space (which in most cases in physics is trivial).

With the Hodge star we will be able to neatly write Maxwell’s equations, and more importantly, generalize them for a large class of physical fields: gauge fields.

References

• Báez, J. C. and Muniain, J. P. (1994). Gauge Fields, Knots, and Gravity, World Scientific. Section I.5. Honestly I don’t even know why you’d read this post, go and read Báez instead.

• Quintero Vélez, A. (2018). Notas de Fundamentos Matemáticos de las Teorías de Campos Gauge.

• Fecko, M. (2006). Differential Geometry and Lie Groups for Physicists. Cambridge University Press. This is a great book with great humor. Chapter 5 is a good introduction to differential forms. It is a problem-driven book.

• Conrad, B. Notes for Math 396: Tensor Algebras, Tensor Pairings, and Duality.http://virtualmath1.stanford.edu/~conrad/diffgeomPage/handouts/tensor.pdf